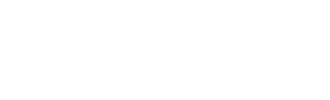摩擦

※スマホでご覧の方は文中の「右図」を「下図」に読み替えてください。

今回は力学の第２弾ということで「摩擦」を取り扱っていきます。

身の回りで摩擦ってどんな場面で登場しますか？

車のブレーキ、消しゴム、寒風摩擦。

なんかもっと良さそうな例がある気がしますが、まあいいでしょう。

身近にある現象の割には、いざ学問のなかで取り扱うと苦手な人が多い。

そんな印象があります。

でも大丈夫！　摩擦で覚えることはほとんどありません。

なんなら前回の力の矢印よりは簡単です。

早速やっていきましょう。

摩擦とはなんぞや？

摩擦力とはそもそもどんな力でしょうか。

結論から言うと、「動こうとするのを邪魔する力」です。

右図を見てください。

右図はざらざらとした粗い床の上の箱を押す図です。

箱は押す手から右に力を受けているので右に動こうとしますが摩擦力はそれを邪魔します。

つまり摩擦力は左むきです。

問題なのは摩擦力の大きさはどれくらいかという話です。

摩擦力の大きさ

摩擦力は動こうとするのを邪魔する、と説明しましたね。

ですので基本的に摩擦は

「物体が受けている力を相殺する大きさ」で働きます。

手から10Nの力を受けているなら10N、20Nなら20N。

めちゃめちゃ簡単です。

では何が摩擦をわかりづらくするのか？

それは摩擦力の“限界"なんですね。

摩擦力には限界がある

身近なもので試して欲しいです。

机にある重いものに優しく触れて、じわーっと力をかけていく。

じわーっと力を増やしていく間、同時に摩擦力もじわーっと同じだけ増えていきます。

ところが、かける力を増やしていくとどこかでズッと動き出しちゃいますよね。

その動き出す直前が摩擦力の限界です。

グラフで説明しましょう。

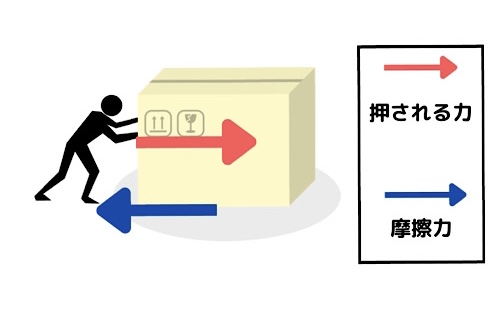
横軸が手から受ける力、縦軸が働く摩擦力です。

横軸が0のところから指でグラフをなぞりながら説明を読んでください。

はじめは受ける力が大きくなる（横軸でいうと右に進む）につれて摩擦力も大きくなります。

（受ける力と摩擦力は同じ大きさなので当たり前ですね。）

ところが、とあるタイミングでガクッと下に落ちてしまいます。

そのタイミングこそがまさに摩擦の限界で、いわば摩擦の心が折れた瞬間です。

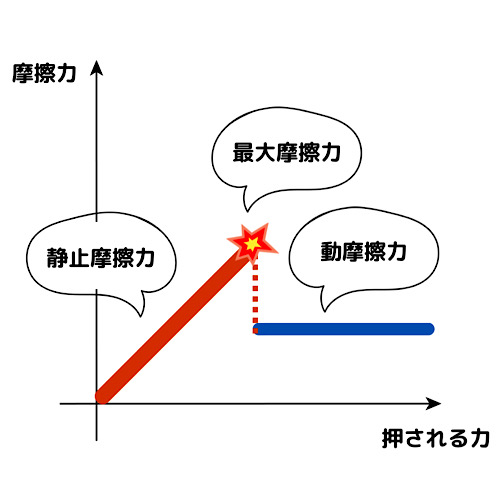
最大摩擦力と動摩擦力

その摩擦力の心が折れる直前を「最大摩擦力」と呼びます。

式にして\(F=μN\)、(最大摩擦力)＝(静止摩擦係数)×(垂直抗力)です。

摩擦が限界を迎えた後は物は動き出します。

押す力に耐えきれなくなったわけです。

そのあとは摩擦はグレたかのように一定の値しか働きません。

これを動摩擦力と呼び

\(F=μ’N\)、(動く摩擦力)＝(動摩擦係数)×(垂直抗力)

となります。

式の形は最大摩擦力とほとんど一緒ですね。

さいごに

摩擦は本当にこれだけで終わりです。

でも今回の内容をわかっていない方が本当に多い。

グラフのイメージが頭に入っていればまず間違いはないのでしっかりマスターしていただければと思います。